Working with lagged variables Regression equations that use time series data often contain lagged variables. For example, consider the regression equation:     Yt = 0 + 1 Yt-1 + 2 Xt + et     for t = 2,...,T where et is a random error term and the total number of observations in the data set is T. This equation contains a lagged dependent variable as an explanatory variable. This is called an autoregressive model or a dynamic model. Note that the sample period is adjusted to start at observation 2. This is because the first observation is "lost" when a lagged variable is required. So the estimation now uses T-1 observations. Another example of a model with lagged variables is:     Yt = 0 + 1 Xt + 2 Xt-1 + 3 Xt-2 + 4 Xt-3 + ut     for t = 4,...,T This model includes current and lagged values of the explanatory variables as regressors. This is called a distributed-lag model. In SHAZAM lagged variables are created by using the GENR command with the LAG function. For a 1-period lag, the command format is: GENR newvar=LAG(var) In general, for an n-period lag, the command format is: GENR newvar=LAG(var,n) where n is the number of lags required. Some important rules must be followed when the LAG function is used. When lags are taken SHAZAM typically sets the initial undefined observations to 0. Therefore, the SAMPLE command must be adjusted to ensure that the subsequent analysis will not include the 0 observations. The time series data must be ordered with the earliest observation as the first observation and the most recent observation as the final observation in the data set. If the left-hand side variable has the same name as the variable in the LAG function then a recursive calculation is implemented. For example, suppose capital stock is to be computed as: CAPITAL(t) = CAPITAL(t-1) + INVEST(t) and the initial capital stock is 25.3. The capital stock series can be computed with the SHAZAM commands: GENR CAPITAL=25.3 SAMPLE 2 T GENR CAPITAL=LAG(CAPITAL)+INVEST Example - Regression with a Lagged Dependent Variable This example uses a data set on monthly sales and advertising expenditures of a dietary weight control product. It is expected that the impact of advertising expenditures (variable name ADVERT) on sales (variable name SALES) will be distributed over a number of months. A model that captures the lagged advertising effects is:     SALESt = + SALESt-1 + ADVERTt + et     for   t = 2,...,T The coefficients , , and can be estimated by the method of ordinary least squares. However, the presence of the lagged dependent variable means that the OLS estimation rule does not give a linear unbiased estimator. It follows that hypothesis testing will only be approximately valid. A result that can be established is that if the error process is serially uncorrelated then the lagged dependent variable will be uncorrelated with the current period error and the OLS estimator will be consistent (close to the true parameter value with high probability in large samples). By repeated substitution for SALESt-1 it is found that an increase of 1 unit in advertising in month t leads to an increase in sales of: in period t, in period t+1, 2 in period t+2, 3 in period t+3,   etc. With || < 1 this gives a pattern of exponentially declining impacts as time goes on. The total increase in sales over all current and future time periods is the sum:       (1 + + 2 + 3 + . . . )   =   / (1 - ) This is the result for the sum of an infinite geometric series when || < 1. After only k time periods the effect is:       (1 + + . . . + k )   =   (1 - k+1 ) / (1 - ) Thus at time k, the percentage of the total advertising effect realized is:         100 (1 - k+1 ) % The above can be solved to find the time period k at which 100p percent of the impact on sales is expected. This gives:         k = log(1 - p) / log() - 1 The SHAZAM commands (filename: SALES.SHA) for equation estimation and analysis of the results follow. SAMPLE 1 36 READ (SALES.txt) SALES ADVERT GENR L1SALES=LAG(SALES) * List the data and take a look PRINT SALES L1SALES ADVERT * Adjust the sample period SAMPLE 2 36 OLS SALES L1SALES ADVERT / COEF=BETA * Analyze the effect of a 1 unit increase in advertising. GEN1 A=BETA:1 GEN1 B=BETA:2 * Get the total impact of advertising on all future sales. GEN1 TOTAL = B/(1-A) * Find the time period at which 95% of the impact is expected. GEN1 P95 = LOG(1-.95)/LOG(A) - 1 PRINT TOTAL P95 * Find the expected increases in sales for up to 6 months ahead. SAMPLE 1 7 GENR AHEAD=TIME(-1) GENR IMPACT = B*(A**AHEAD) PRINT AHEAD IMPACT STOP The SHAZAM output can be viewed. The estimated equation is:       SALESt = 7.45 + 0.528 SALESt-1 + 0.146 ADVERTt + êt The results show that a 1 unit increase in advertising gives a 0.146 unit increase in sales in the current month. However, the total expected increase in sales in the current and all future months is calculated as: 0.146 / (1 - 0.528) = 0.310 The time period at which 95% of the effect is realized is found as: log(1 - 0.95)/log(0.528) - 1 = 3.69 This implies that after 4 months more than 95% of the advertising effect will be reflected in the sales performance. The figure below shows the month by month sales response to advertising in the current month. 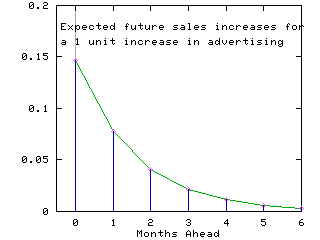[SHAZAM Guide home] SHAZAM output - Regression with a Lagged Dependent Variable |_SAMPLE 1 36 |_READ (SALES.txt) SALES ADVERT UNIT 88 IS NOW ASSIGNED TO: SALES.txt 2 VARIABLES AND 36 OBSERVATIONS STARTING AT OBS 1 |_GENR L1SALES=LAG(SALES) ..NOTE.LAG VALUE IN UNDEFINED OBSERVATIONS SET TO ZERO |_* List the data and take a look |_PRINT SALES L1SALES ADVERT SALES L1SALES ADVERT 12.00000 .0000000 15.00000 20.50000 12.00000 16.00000 21.00000 20.50000 18.00000 15.50000 21.00000 27.00000 15.30000 15.50000 21.00000 23.50000 15.30000 49.00000 24.50000 23.50000 21.00000 21.30000 24.50000 22.00000 23.50000 21.30000 28.00000 28.00000 23.50000 36.00000 24.00000 28.00000 40.00000 15.50000 24.00000 3.000000 17.30000 15.50000 21.00000 25.30000 17.30000 29.00000 25.00000 25.30000 62.00000 36.50000 25.00000 65.00000 36.50000 36.50000 46.00000 29.60000 36.50000 44.00000 30.50000 29.60000 33.00000 28.00000 30.50000 62.00000 26.00000 28.00000 22.00000 21.50000 26.00000 12.00000 19.70000 21.50000 24.00000 19.00000 19.70000 3.000000 16.00000 19.00000 5.000000 20.70000 16.00000 14.00000 26.50000 20.70000 36.00000 30.60000 26.50000 40.00000 32.30000 30.60000 49.00000 29.50000 32.30000 7.000000 28.30000 29.50000 52.00000 31.30000 28.30000 65.00000 32.30000 31.30000 17.00000 26.40000 32.30000 5.000000 23.40000 26.40000 17.00000 16.40000 23.40000 1.000000 |_* Adjust the sample period |_SAMPLE 2 36 |_OLS SALES L1SALES ADVERT / COEF=BETA OLS ESTIMATION 35 OBSERVATIONS DEPENDENT VARIABLE = SALES ...NOTE..SAMPLE RANGE SET TO: 2, 36 R-SQUARE = .6720 R-SQUARE ADJUSTED = .6515 VARIANCE OF THE ESTIMATE-SIGMA**2 = 12.142 STANDARD ERROR OF THE ESTIMATE-SIGMA = 3.4845 SUM OF SQUARED ERRORS-SSE= 388.53 MEAN OF DEPENDENT VARIABLE = 24.606 LOG OF THE LIKELIHOOD FUNCTION = -91.7859 VARIABLE ESTIMATED STANDARD T-RATIO PARTIAL STANDARDIZED ELASTICITY NAME COEFFICIENT ERROR 32 DF P-VALUE CORR. COEFFICIENT AT MEANS L1SALES .52793 .1021 5.170 .000 .675 .5478 .5252 ADVERT .14647 .3308E-01 4.428 .000 .616 .4692 .1721 CONSTANT 7.4469 2.470 3.015 .005 .470 .0000 .3027 |_* Analyze the effect of a 1 unit increase in advertising. |_GEN1 A=BETA:1 |_GEN1 B=BETA:2 |_* Get the total impact of advertising on all future sales. |_GEN1 TOTAL = B/(1-A) |_* Find the time period at which 95% of the impact is expected. |_GEN1 P95 = LOG(1-.95)/LOG(A) - 1 |_PRINT TOTAL P95 TOTAL .3102750 P95 3.689629 |_* Find the expected increases in sales for up to 6 months ahead. |_SAMPLE 1 7 |_GENR AHEAD=TIME(-1) |_GENR IMPACT = B*(A**AHEAD) |_PRINT AHEAD IMPACT AHEAD IMPACT .0000000 .1464728 1.000000 .7732677E-01 2.000000 .4082280E-01 3.000000 .2155141E-01 4.000000 .1137755E-01 5.000000 .6006502E-02 6.000000 .3170988E-02 |_STOP [SHAZAM Guide home]