Logit and Probit Analysis
When the dependent variable is a 0-1 binary variable the logit
or probit model estimation methods can be used.
In SHAZAM, these methods are implemented with the
LOGIT and PROBIT commands.
The logit model is discussed and illustrated here.
The probit model can be implemented in a similar style.
For the LOGIT command,
the general command format is:
LOGIT depvar indeps / options
|
where depvar is a 0-1 binary dependent variable, indeps is a list of the explanatory variables and options is a list of desired options. The list of options is described in the SHAZAM User's Reference Manual.
The logit model assumes that the response probability has the form:
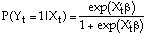
An equivalent form can be stated by noting that:
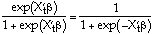
The function guarantees probabilities in the (0,1) range.
The logit form also gives a plausible shape for the marginal effects.
That is, for a continuous variable
The estimation problem is to find estimates of the unknown parameters
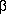 .
.
Example
A data set on voting decisions for a school budget is available. The question of interest is: what factors influence the probability of a yes vote ? This question can be answered by interpreting the estimation results from a logit model. SHAZAM commands are given below.
SAMPLE 1 95 READ (school.txt) PUB12 PUB34 PUB5 PRIV YEARS SCHOOL & LOGINC PTCON YESVM * The income and tax variables are in logarithms -- take anti-logs * to express the variables in thousands of $. * Income GENR INCOME=EXP(LOGINC)/1000 * Property taxes GENR TAX=EXP(PTCON)/1000 * LOGIT estimation. LOGIT YESVM PUB12 PUB34 PUB5 PRIV YEARS SCHOOL INCOME TAX * Now use the log transformed form of income and taxes. LOGIT YESVM PUB12 PUB34 PUB5 PRIV YEARS SCHOOL LOGINC PTCON * Use the LOG option to compute elasticities and marginal effects * assuming log-transformed variables. LOGIT YESVM PUB12 PUB34 PUB5 PRIV YEARS SCHOOL LOGINC PTCON / LOG COEF=BETA STOP |
The first model estimation includes the income and property tax variables in levels. The second model estimation includes log transformations of the income and property tax variables. Rubinfeld (1977, p. 35) comments: "The inclusion of logarithmic income and price terms resulted in a better fit than the inclusion of linear forms of the variables".
The SHAZAM output can be viewed. The results are discussed in the following sections:
- Model Estimation by the Method of Maximum Likelihood
- Interpretation of the Results
- Overall Significance and Goodness of Fit Measures
- Predicting Probabilities
- Testing for Heteroskedasticity
References
Good textbook discussion is:
William Greene, Econometric Analysis.Jeffrey M. Wooldridge, Introductory Econometrics: A Modern Approach.
References with more technical details are:
R. Davidson and J.G. MacKinnon, "Convenient Specification Tests for Logit and Probit Models", Journal of Econometrics, Vol 25, 1984, pp. 241-262.D. A. Hensher and L. W. Johnson, Applied Discrete-Choice Modelling, John Wiley & Sons, 1981.
G. S. Maddala, Limited-dependent and Qualitative Variables in Econometrics, Cambridge University Press, 1983.
Kenneth Train, Qualitative Choice Analysis: Theory, Econometrics and an Application to Automobile Demand, MIT Press, 1986.
 [SHAZAM Guide home]
[SHAZAM Guide home]
SHAZAM output
|_SAMPLE 1 95
|_READ (school.txt) PUB12 PUB34 PUB5 PRIV YEARS SCHOOL &
| LOGINC PTCON YESVM
UNIT 88 IS NOW ASSIGNED TO: school.txt
9 VARIABLES AND 95 OBSERVATIONS STARTING AT OBS 1
|_* The income and tax variables are in logarithms -- take anti-logs
|_* to express the variables in thousands of $.
|_* Income
|_GENR INCOME=EXP(LOGINC)/1000
|_* Property taxes
|_GENR TAX=EXP(PTCON)/1000
|_* LOGIT estimation.
|_LOGIT YESVM PUB12 PUB34 PUB5 PRIV YEARS SCHOOL INCOME TAX
LOGIT ANALYSIS DEPENDENT VARIABLE =YESVM CHOICES = 2
95. TOTAL OBSERVATIONS
59. OBSERVATIONS AT ONE
36. OBSERVATIONS AT ZERO
25 MAXIMUM ITERATIONS
CONVERGENCE TOLERANCE =0.00100
LOG OF LIKELIHOOD WITH CONSTANT TERM ONLY = -63.037
BINOMIAL ESTIMATE = 0.6211
ITERATION 0 LOG OF LIKELIHOOD FUNCTION = -63.037
ITERATION 1 ESTIMATES
0.54133 0.97999 0.39823 -0.23810 -0.28618E-01 1.1845
0.49110E-01 -1.6498 0.68486
ITERATION 1 LOG OF LIKELIHOOD FUNCTION = -55.958
ITERATION 2 ESTIMATES
0.61000 1.1179 0.44480 -0.30742 -0.31099E-01 1.7144
0.63240E-01 -2.0213 0.75025
ITERATION 2 LOG OF LIKELIHOOD FUNCTION = -55.560
ITERATION 3 ESTIMATES
0.62370 1.1363 0.44904 -0.31404 -0.31469E-01 1.8634
0.65039E-01 -2.0686 0.75393
ITERATION 3 LOG OF LIKELIHOOD FUNCTION = -55.548
ITERATION 4 ESTIMATES
0.62413 1.1368 0.44921 -0.31413 -0.31480E-01 1.8724
0.65077E-01 -2.0696 0.75389
ASYMPTOTIC WEIGHTED
VARIABLE ESTIMATED STANDARD T-RATIO ELASTICITY AGGREGATE
NAME COEFFICIENT ERROR AT MEANS ELASTICITY
PUB12 0.62413 0.66847 0.93366 0.10588 0.10248
PUB34 1.1368 0.74861 1.5185 0.12577 0.10148
PUB5 0.44921 1.2500 0.35937 0.66268E-02 0.61577E-02
PRIV -0.31413 0.77985 -0.40281 -0.11585E-01 -0.11295E-01
YEARS -0.31480E-01 0.26096E-01 -1.2063 -0.93925E-01 -0.88468E-01
SCHOOL 1.8724 1.1255 1.6636 0.75959E-01 0.27663E-01
INCOME 0.65077E-01 0.35634E-01 1.8263 0.52655 0.48027
TAX -2.0696 1.0383 -1.9932 -0.78308 -0.73375
CONSTANT 0.75389 1.1352 0.66411 0.26413 0.24491
SCALE FACTOR = 0.22761
VARIABLE MARGINAL ----- PROBABILITIES FOR A TYPICAL CASE -----
NAME EFFECT CASE X=0 X=1 MARGINAL
VALUES EFFECT
PUB12 0.14206 0.0000 0.43871 0.59333 0.15462
PUB34 0.25874 0.0000 0.43871 0.70897 0.27026
PUB5 0.10224 0.0000 0.43871 0.55053 0.11182
PRIV -0.71499E-01 0.0000 0.43871 0.36342 -0.75286E-01
YEARS -0.71652E-02 8.5158
SCHOOL 0.42617 0.0000 0.43871 0.83562 0.39691
INCOME 0.14812E-01 23.094
TAX -0.47105 1.0800
LOG-LIKELIHOOD FUNCTION = -55.548
LOG-LIKELIHOOD(0) = -63.037
LIKELIHOOD RATIO TEST = 14.9788 WITH 8 D.F. P-VALUE= 0.05956
ESTRELLA R-SQUARE 0.15452
MADDALA R-SQUARE 0.14587
CRAGG-UHLER R-SQUARE 0.19853
MCFADDEN R-SQUARE 0.11881
ADJUSTED FOR DEGREES OF FREEDOM 0.36838E-01
APPROXIMATELY F-DISTRIBUTED 0.15168 WITH 8 AND 9 D.F.
CHOW R-SQUARE 0.13244
PREDICTION SUCCESS TABLE
ACTUAL
0 1
0 14. 6.
PREDICTED 1 22. 53.
NUMBER OF RIGHT PREDICTIONS = 67.0
PERCENTAGE OF RIGHT PREDICTIONS = 0.70526
NAIVE MODEL PERCENTAGE OF RIGHT PREDICTIONS = 0.62105
EXPECTED OBSERVATIONS AT 0 = 36.0 OBSERVED = 36.0
EXPECTED OBSERVATIONS AT 1 = 59.0 OBSERVED = 59.0
SUM OF SQUARED "RESIDUALS" = 19.397
WEIGHTED SUM OF SQUARED "RESIDUALS" = 89.109
HENSHER-JOHNSON PREDICTION SUCCESS TABLE
OBSERVED OBSERVED
PREDICTED CHOICE COUNT SHARE
ACTUAL 0 1
0 16.718 19.282 36.000 0.379
1 19.282 39.718 59.000 0.621
PREDICTED COUNT 36.000 59.000 95.000 1.000
PREDICTED SHARE 0.379 0.621 1.000
PROP. SUCCESSFUL 0.464 0.673 0.594
SUCCESS INDEX 0.085 0.052 0.065
PROPORTIONAL ERROR 0.000 0.000
NORMALIZED SUCCESS INDEX 0.138
|_* Now use the log transformed form of income and taxes.
|_LOGIT YESVM PUB12 PUB34 PUB5 PRIV YEARS SCHOOL LOGINC PTCON
LOGIT ANALYSIS DEPENDENT VARIABLE =YESVM CHOICES = 2
95. TOTAL OBSERVATIONS
59. OBSERVATIONS AT ONE
36. OBSERVATIONS AT ZERO
25 MAXIMUM ITERATIONS
CONVERGENCE TOLERANCE =0.00100
LOG OF LIKELIHOOD WITH CONSTANT TERM ONLY = -63.037
BINOMIAL ESTIMATE = 0.6211
ITERATION 0 LOG OF LIKELIHOOD FUNCTION = -63.037
ITERATION 1 ESTIMATES
0.45375 0.92076 0.43035 -0.28835 -0.23416E-01 1.3330
1.6059 -1.7546 -3.7958
ITERATION 1 LOG OF LIKELIHOOD FUNCTION = -54.139
ITERATION 2 ESTIMATES
0.55298 1.0944 0.50979 -0.32984 -0.25855E-01 2.1655
2.0427 -2.2551 -4.7103
ITERATION 2 LOG OF LIKELIHOOD FUNCTION = -53.370
ITERATION 3 ESTIMATES
0.58166 1.1250 0.52500 -0.33987 -0.26178E-01 2.5635
2.1706 -2.3799 -5.1361
ITERATION 3 LOG OF LIKELIHOOD FUNCTION = -53.304
ITERATION 4 ESTIMATES
0.58362 1.1261 0.52605 -0.34139 -0.26129E-01 2.6239
2.1869 -2.3942 -5.2003
ITERATION 4 LOG OF LIKELIHOOD FUNCTION = -53.303
ITERATION 5 ESTIMATES
0.58364 1.1261 0.52606 -0.34142 -0.26127E-01 2.6250
2.1872 -2.3945 -5.2014
ASYMPTOTIC WEIGHTED
VARIABLE ESTIMATED STANDARD T-RATIO ELASTICITY AGGREGATE
NAME COEFFICIENT ERROR AT MEANS ELASTICITY
PUB12 0.58364 0.68778 0.84858 0.93986E-01 0.91051E-01
PUB34 1.1261 0.76820 1.4659 0.11827 0.96460E-01
PUB5 0.52606 1.2693 0.41445 0.73664E-02 0.69375E-02
PRIV -0.34142 0.78299 -0.43605 -0.11952E-01 -0.12037E-01
YEARS -0.26127E-01 0.26934E-01 -0.97006 -0.73996E-01 -0.68592E-01
SCHOOL 2.6250 1.4101 1.8616 0.10108 0.28999E-01
LOGINC 2.1872 0.78781 2.7763 7.2529 6.7561
PTCON -2.3945 1.0813 -2.2145 -5.5262 -5.1745
CONSTANT -5.2014 7.5503 -0.68890 -1.7298 -1.6137
SCALE FACTOR = 0.22197
VARIABLE MARGINAL ----- PROBABILITIES FOR A TYPICAL CASE -----
NAME EFFECT CASE X=0 X=1 MARGINAL
VALUES EFFECT
PUB12 0.12955 0.0000 0.44231 0.58706 0.14476
PUB34 0.24996 0.0000 0.44231 0.70978 0.26747
PUB5 0.11677 0.0000 0.44231 0.57304 0.13073
PRIV -0.75785E-01 0.0000 0.44231 0.36049 -0.81814E-01
YEARS -0.57995E-02 8.5158
SCHOOL 0.58267 0.0000 0.44231 0.91631 0.47400
LOGINC 0.48548 9.9711
PTCON -0.53150 6.9395
LOG-LIKELIHOOD FUNCTION = -53.303
LOG-LIKELIHOOD(0) = -63.037
LIKELIHOOD RATIO TEST = 19.4681 WITH 8 D.F. P-VALUE= 0.01255
ESTRELLA R-SQUARE 0.19956
MADDALA R-SQUARE 0.18529
CRAGG-UHLER R-SQUARE 0.25218
MCFADDEN R-SQUARE 0.15442
ADJUSTED FOR DEGREES OF FREEDOM 0.75759E-01
APPROXIMATELY F-DISTRIBUTED 0.20544 WITH 8 AND 9 D.F.
CHOW R-SQUARE 0.17197
PREDICTION SUCCESS TABLE
ACTUAL
0 1
0 18. 7.
PREDICTED 1 18. 52.
NUMBER OF RIGHT PREDICTIONS = 70.0
PERCENTAGE OF RIGHT PREDICTIONS = 0.73684
NAIVE MODEL PERCENTAGE OF RIGHT PREDICTIONS = 0.62105
EXPECTED OBSERVATIONS AT 0 = 36.0 OBSERVED = 36.0
EXPECTED OBSERVATIONS AT 1 = 59.0 OBSERVED = 59.0
SUM OF SQUARED "RESIDUALS" = 18.513
WEIGHTED SUM OF SQUARED "RESIDUALS" = 86.839
HENSHER-JOHNSON PREDICTION SUCCESS TABLE
OBSERVED OBSERVED
PREDICTED CHOICE COUNT SHARE
ACTUAL 0 1
0 17.591 18.409 36.000 0.379
1 18.409 40.591 59.000 0.621
PREDICTED COUNT 36.000 59.000 95.000 1.000
PREDICTED SHARE 0.379 0.621 1.000
PROP. SUCCESSFUL 0.489 0.688 0.612
SUCCESS INDEX 0.110 0.067 0.083
PROPORTIONAL ERROR 0.000 0.000
NORMALIZED SUCCESS INDEX 0.177
|_* Use the LOG option to compute elasticities and marginal effects
|_* assuming log-transformed variables.
|_LOGIT YESVM PUB12 PUB34 PUB5 PRIV YEARS SCHOOL LOGINC PTCON / LOG
LOGIT ANALYSIS DEPENDENT VARIABLE =YESVM CHOICES = 2
95. TOTAL OBSERVATIONS
59. OBSERVATIONS AT ONE
36. OBSERVATIONS AT ZERO
25 MAXIMUM ITERATIONS
CONVERGENCE TOLERANCE =0.00100
LOG OF LIKELIHOOD WITH CONSTANT TERM ONLY = -63.037
BINOMIAL ESTIMATE = 0.6211
ITERATION 0 LOG OF LIKELIHOOD FUNCTION = -63.037
ITERATION 1 ESTIMATES
0.45375 0.92076 0.43035 -0.28835 -0.23416E-01 1.3330
1.6059 -1.7546 -3.7958
ITERATION 1 LOG OF LIKELIHOOD FUNCTION = -54.139
ITERATION 2 ESTIMATES
0.55298 1.0944 0.50979 -0.32984 -0.25855E-01 2.1655
2.0427 -2.2551 -4.7103
ITERATION 2 LOG OF LIKELIHOOD FUNCTION = -53.370
ITERATION 3 ESTIMATES
0.58166 1.1250 0.52500 -0.33987 -0.26178E-01 2.5635
2.1706 -2.3799 -5.1361
ITERATION 3 LOG OF LIKELIHOOD FUNCTION = -53.304
ITERATION 4 ESTIMATES
0.58362 1.1261 0.52605 -0.34139 -0.26129E-01 2.6239
2.1869 -2.3942 -5.2003
ITERATION 4 LOG OF LIKELIHOOD FUNCTION = -53.303
ITERATION 5 ESTIMATES
0.58364 1.1261 0.52606 -0.34142 -0.26127E-01 2.6250
2.1872 -2.3945 -5.2014
ELASTICITIES ASSUME LOG-TRANSFORMED VARIABLES
ASYMPTOTIC WEIGHTED
VARIABLE ESTIMATED STANDARD T-RATIO ELASTICITY AGGREGATE
NAME COEFFICIENT ERROR AT MEANS ELASTICITY
PUB12 0.58364 0.68778 0.84858 0.19410 0.18107
PUB34 1.1261 0.76820 1.4659 0.37451 0.34937
PUB5 0.52606 1.2693 0.41445 0.17495 0.16321
PRIV -0.34142 0.78299 -0.43605 -0.11355 -0.10592
YEARS -0.26127E-01 0.26934E-01 -0.97006 -0.86893E-02 -0.81059E-02
SCHOOL 2.6250 1.4101 1.8616 0.87301 0.81439
LOGINC 2.1872 0.78781 2.7763 0.72739 0.67856
PTCON -2.3945 1.0813 -2.2145 -0.79633 -0.74287
CONSTANT -5.2014 7.5503 -0.68890 -1.7298 -1.6137
SCALE FACTOR = 0.22197
MARGINAL EFFECTS ASSUME ALL VARIABLES ARE LOG-TRANSFORMED
(EXCEPT DUMMY VARIABLES)
VARIABLE MARGINAL ----- PROBABILITIES FOR A TYPICAL CASE -----
NAME EFFECT CASE X=0 X=1 MARGINAL
VALUES EFFECT
PUB12 0.12955 0.0000 0.44231 0.58706 0.14476
PUB34 0.24996 0.0000 0.44231 0.70978 0.26747
PUB5 0.11677 0.0000 0.44231 0.57304 0.13073
PRIV -0.75785E-01 0.0000 0.44231 0.36049 -0.81814E-01
YEARS -0.28859E-21 8.5158
SCHOOL 0.58267 0.0000 0.44231 0.91631 0.47400
LOGINC 0.21022E-04 9.9711
PTCON -0.49214E-03 6.9395
LOG-LIKELIHOOD FUNCTION = -53.303
LOG-LIKELIHOOD(0) = -63.037
LIKELIHOOD RATIO TEST = 19.4681 WITH 8 D.F. P-VALUE= 0.01255
ESTRELLA R-SQUARE 0.19956
MADDALA R-SQUARE 0.18529
CRAGG-UHLER R-SQUARE 0.25218
MCFADDEN R-SQUARE 0.15442
ADJUSTED FOR DEGREES OF FREEDOM 0.75759E-01
APPROXIMATELY F-DISTRIBUTED 0.20544 WITH 8 AND 9 D.F.
CHOW R-SQUARE 0.17197
PREDICTION SUCCESS TABLE
ACTUAL
0 1
0 18. 7.
PREDICTED 1 18. 52.
NUMBER OF RIGHT PREDICTIONS = 70.0
PERCENTAGE OF RIGHT PREDICTIONS = 0.73684
NAIVE MODEL PERCENTAGE OF RIGHT PREDICTIONS = 0.62105
EXPECTED OBSERVATIONS AT 0 = 36.0 OBSERVED = 36.0
EXPECTED OBSERVATIONS AT 1 = 59.0 OBSERVED = 59.0
SUM OF SQUARED "RESIDUALS" = 18.513
WEIGHTED SUM OF SQUARED "RESIDUALS" = 86.839
HENSHER-JOHNSON PREDICTION SUCCESS TABLE
OBSERVED OBSERVED
PREDICTED CHOICE COUNT SHARE
ACTUAL 0 1
0 17.591 18.409 36.000 0.379
1 18.409 40.591 59.000 0.621
PREDICTED COUNT 36.000 59.000 95.000 1.000
PREDICTED SHARE 0.379 0.621 1.000
PROP. SUCCESSFUL 0.489 0.688 0.612
SUCCESS INDEX 0.110 0.067 0.083
PROPORTIONAL ERROR 0.000 0.000
NORMALIZED SUCCESS INDEX 0.177
|_STOP
 [SHAZAM Guide home]
[SHAZAM Guide home]