SHAZAM Portfolio Selection

Portfolio Selection

The PORTFOLIO command provides features for calculating efficient portfolios.

Example

Berndt [1991, Chapter 2] provides a data set of monthly returns for a number of companies for the period January 1978 to December 1987. From this data set, a file (filename: P.txt) was prepared with returns for Mobil, IBM, Weyerhauser and Citicorp as well as the return on 30-day Treasury Bills (a measure of the risk-free return) and a value-weighted composite monthly market return based on all stocks listed at the New York and American Stock Exchanges.

The SHAZAM commands below solve a portfolio selection problem. 

SAMPLE 1 120
READ (P.txt) DATE MOBIL IBM WEYER CITCRP MARKET RKFREE / SKIPLINES=1
* Convert to percentages
GENR MOBIL=100*MOBIL
GENR IBM=100*IBM
GENR WEYER=100*WEYER
GENR CITCRP=100*CITCRP
* Set a risk-free rate of return
GEN1 RF=100*(RKFREE:120)
PORTFOLIO MOBIL IBM WEYER CITCRP / INRATES RISKFREE=RF EQUALW PFRONT &
       GRAPHDATA GRAPHLINE 
STOP

Below is SHAZAM output generated by the PORTFOLIO command. 

 |_PORTFOLIO MOBIL IBM WEYER CITCRP / INRATES RISKFREE=RF EQUALW PFRONT &
 |        GRAPHDATA GRAPHLINE
 PORTFOLIO ANALYSIS - RATES OF RETURN     4 ASSETS        120 OBSERVATIONS
 MEAN RISKFREE RATE OF RETURN =  0.27700
 VARIABLE      MEAN        ST.DEV      SHARPE
 MOBIL      1.6192       8.0308      0.16713
 IBM       0.96167       5.9024      0.11600
 WEYER     0.96333       8.5066      0.80682E-01
 CITCRP     1.1858       8.0972      0.11224

 COVARIANCE MATRIX
 MOBIL      64.493
 IBM        15.225       34.838
 WEYER      26.403       24.694       72.363
 CITCRP     20.227       20.250       37.195       65.564
              MOBIL        IBM          WEYER        CITCRP

 EFFICIENT PORTFOLIOS
          MINIMUMVARIANCE   RISKFREE=ZERO       RETURN=ZERO       ACTUAL
  MEAN       1.1521            1.3300           0.44409E-15        1.1825
  VARIANCE   27.751            32.037            207.44            32.828
  STDEV      5.2680            5.6602            14.403            5.7296
  SHARPE    0.16612           0.18604          -0.19233E-01       0.15804
 PORTFOLIO WEIGHTS
 MOBIL      0.23486           0.48422           -1.3797           0.25000
 IBM        0.59096           0.39925            1.8322           0.25000
 WEYER      0.13607E-01      -0.10732           0.79655           0.25000
 CITCRP     0.16057           0.22385          -0.24910           0.25000

The figure below shows the minimum-variance risk-return frontier. The x-axis measures the standard deviation of return.

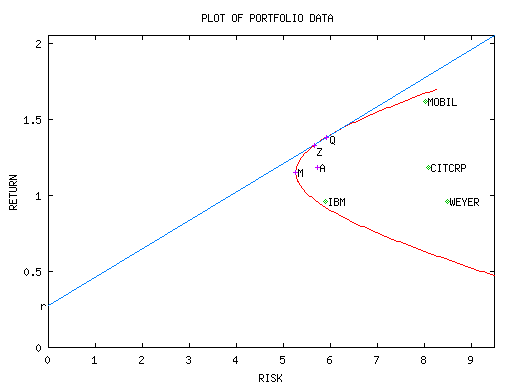
The portfolios marked M and Z are the MINIMUMVARIANCE and RISKFREE=ZERO portfolios respectively. The curve that extends upward from point M gives the efficient frontier. That is, all portfolios on the efficient frontier have greater expected return than the portfolio with the global minimum variance.

The portfolio A is the equal-weighted portfolio calculated with the EQUALWEIGHT option and reported on the SHAZAM output in the ACTUAL column. Clearly, this is not an efficient portfolio since it is possible to find an alternative portfolio with the same risk but a higher expected return.

The straight line with an intercept at the risk-free rate of return r that is tangential to the efficient frontier at point Q has a slope that is the maximimum Sharpe ratio of all possible portfolios.

Home [SHAZAM Guide home]