Logit Estimation Results     Model Estimation by the Method of Maximum Likelihood The coefficients of the logit model are estimated by the method of maximum likelihood estimation. The likelihood function L gives the joint probability density function, or likelihood, of observing the sample Y1, Y2, . . . YN . The coefficient estimates are the values that maximize the value of the log likelihood function logL. Solution is obtained by a numerical optimization algorithm. The first step is to set some starting values for the coefficients. A sensible approach is to set all slope coefficients to zero. In this case, the probability that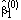 Yt is one is estimated by the sample proportion S / N (the binomial estimate), where S is the number of successes (observations at one) observed in the N sample observations. 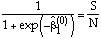The starting value for the intercept, denoted by , is then obtained by solving:       The next step (iteration 1) is to apply an updating rule to update the starting values to a new set of coefficient estimates. In successive iterations, coefficient estimates are updated from the previous iteration. The iterations stop when there is little improvement. This is called convergence. For the logit model, convergence is usually achieved in 4 or 5 iterations. Furthermore, the form of the log-likelihood function for the logit model guarantees that different starting values will lead to unique maximum likelihood estimates. This attractive property makes the logit model an estimation method that can be used with some success. A general warning is that if the number of iterations exceeds 10 or 15 then this may be a signal of multicollinearity in the data set. A result may be relatively high estimated standard errors on the estimation output. For the first model in the school budget voting study, the SHAZAM output below shows that the estimation converged in 4 iterations. LOGIT ANALYSIS DEPENDENT VARIABLE =YESVM CHOICES = 2 95. TOTAL OBSERVATIONS 59. OBSERVATIONS AT ONE 36. OBSERVATIONS AT ZERO 25 MAXIMUM ITERATIONS CONVERGENCE TOLERANCE =0.00100 LOG OF LIKELIHOOD WITH CONSTANT TERM ONLY = -63.037 BINOMIAL ESTIMATE = 0.6211 ITERATION 0 LOG OF LIKELIHOOD FUNCTION = -63.037 ITERATION 1 ESTIMATES 0.54133 0.97999 0.39823 -0.23810 -0.28618E-01 1.1845 0.49110E-01 -1.6498 0.68486 ITERATION 1 LOG OF LIKELIHOOD FUNCTION = -55.958 ITERATION 2 ESTIMATES 0.61000 1.1179 0.44480 -0.30742 -0.31099E-01 1.7144 0.63240E-01 -2.0213 0.75025 ITERATION 2 LOG OF LIKELIHOOD FUNCTION = -55.560 ITERATION 3 ESTIMATES 0.62370 1.1363 0.44904 -0.31404 -0.31469E-01 1.8634 0.65039E-01 -2.0686 0.75393 ITERATION 3 LOG OF LIKELIHOOD FUNCTION = -55.548 ITERATION 4 ESTIMATES 0.62413 1.1368 0.44921 -0.31413 -0.31480E-01 1.8724 0.65077E-01 -2.0696 0.75389 The first part of the above output states that, of 95 observations in the sample, there were 59 yes votes (OBSERVATIONS AT ONE). The proportion of yes votes is the BINOMIAL ESTIMATE:       59 / 95 = 0.6211 The value of the log-likelihood function when all slope coefficients are zero is -63.037. It can be observed that the value of the log-likelihood function increases at each iteration to a final value of -55.548. The estimation output for the school budget voting study also reports the results for a second model estimation where income and property taxes are log-transformed. For this model, the estimation output shows that the value of the log-likelihood function when all slope coefficients are zero (ITERATION 0) is identical to the value reported for the first model where income and property taxes are in level form. However, the iterations progress to a final value of the log-likelihood function of -53.303. This value is higher than the value reported for the first model to give some evidence that the log-transformed variables give a better fit.     Interpretation of the Results Logit estimation results for the first model in the school budget voting study are below: ASYMPTOTIC WEIGHTED VARIABLE ESTIMATED STANDARD T-RATIO ELASTICITY AGGREGATE NAME COEFFICIENT ERROR AT MEANS ELASTICITY PUB12 0.62413 0.66847 0.93366 0.10588 0.10248 PUB34 1.1368 0.74861 1.5185 0.12577 0.10148 PUB5 0.44921 1.2500 0.35937 0.66268E-02 0.61577E-02 PRIV -0.31413 0.77985 -0.40281 -0.11585E-01 -0.11295E-01 YEARS -0.31480E-01 0.26096E-01 -1.2063 -0.93925E-01 -0.88468E-01 SCHOOL 1.8724 1.1255 1.6636 0.75959E-01 0.27663E-01 INCOME 0.65077E-01 0.35634E-01 1.8263 0.52655 0.48027 TAX -2.0696 1.0383 -1.9932 -0.78308 -0.73375 CONSTANT 0.75389 1.1352 0.66411 0.26413 0.24491 SCALE FACTOR = 0.22761 VARIABLE MARGINAL ----- PROBABILITIES FOR A TYPICAL CASE ----- NAME EFFECT CASE X=0 X=1 MARGINAL VALUES EFFECT PUB12 0.14206 0.0000 0.43871 0.59333 0.15462 PUB34 0.25874 0.0000 0.43871 0.70897 0.27026 PUB5 0.10224 0.0000 0.43871 0.55053 0.11182 PRIV -0.71499E-01 0.0000 0.43871 0.36342 -0.75286E-01 YEARS -0.71652E-02 8.5158 SCHOOL 0.42617 0.0000 0.43871 0.83562 0.39691 INCOME 0.14812E-01 23.094 TAX -0.47105 1.0800 Rubinfeld (1977, p. 35) states: The income variable serves as a measure of the capacity of households to consume both private and public goods. On the assumption that local school education is a normal good, we expected, other things equal, that income and the demand for public schools would be positively correlated. In the context of our voting model, this suggests a positive relationship between income and the probability of a yes vote. The logit estimation results can be used to test the above hypothesis. The statistical properties for the maximum likelihood estimator are established for "large" samples (asymptotically). This means that the asymptotic t statistic has an approximate normal distribution in "large" samples. In other words, the results of any hypothesis testing exercise can be considered as approximate when applied to "small" samples. The sign of an estimated coefficient gives the direction of the effect of a change in the explanatory variable on the probability of a success (an observation at one). The positive estimated coefficient on income suggests that an increase in income gives a higher probability of a yes vote. A test of the null hypothesis that the income coefficient is zero against the alternative hypothesis that the income coefficient is positive has a t-test statistic of 1.83. For a one-sided test, the approximate 5% critical value is 1.645. The calculated test statistic exceeds the critical value and therefore the null hypothesis is rejected in favour of the alternative.         Elasticities and Marginal Effects for Roughly Continuous Variables For the logit model, the estimated coefficients do not have a direct economic interpretation. Measures that are familiar to economists are marginal effects and elasticities. First consider the calculation of elasticities. An elasticity gives the percentage change in the probability of a success in response to a one percentage change in the explanatory variable. 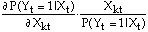For the kth explanatory variable this is obtained using partial derivatives as:       Since the elasticities vary for every observation it is desirable to report a summary measure. A convenient summary measure is to evaluate the elasticity at the sample means of the explanatory variables. This measure is reported as ELASTICITY AT MEANS on the SHAZAM estimation output. A criticism of this measure is that since the elasticities are nonlinear functions of the observed data there is no guarantee that the logit function will pass through the point defined by the sample averages (see the discussion in Train (1986, p. 42)). To address this limitation, Hensher and Johnson (1981, p. 59) propose evaluating the elasticities at every observation and then constructing a weighted average where the predicted probabilities are the weights. This measure is reported on the SHAZAM output as the WEIGHTED AGGREGATE ELASTICITY. Hensher and Johnson note that the elasticity at means measure tends to over-estimate the probability response to a change in an explanatory variable. Using the weighted aggregate elasticity measure, the SHAZAM output for the first model in the school budget voting study shows that, on average, a one percent increase in income gives a 0.48 percent increase in the probability of a yes vote, holding all else constant. The marginal effect of the kth explanatory variable on the response probability is obtained from: 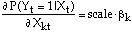          where 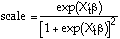  That is, estimates of the marginal effects are calculated by rescaling the estimated coefficients. The scale factor varies with the observed values of X. For reporting purposes, the scale factor can be evaluated at the sample means of the explanatory variables. This value is reported as SCALE FACTOR on the SHAZAM logit estimation output. Greene (2000, p. 816) notes that a preferred method may be to obtain a scale factor by evaluating the expression at every observation and then taking the average. He comments that in "large" samples, by applying the Slutsky theorem, this result will be similar to the result obtained by evaluating the scale factor at the sample means. By inspecting the marginal effects reported on the SHAZAM output for the first model in the school budget voting study it is found that, on average, a $1000 increase in income leads to a 0.015 increase in the probability of a yes vote, holding all else constant. Some cautionary notes are required when interpreting the elasticities and marginal effects discussed above. The formula derived from a partial derivative is meaningful when the explanatory variable of interest is roughly continuous, such as income. The formula do not apply to determining the magnitude of the partial effect from changing a dummy variable from zero to one. That is, the estimated elasticities reported on the SHAZAM output may not have any useful interpretation for dummy explanatory variables. The calculation of marginal effects for dummy explanatory variables is discussed in the next section. It should also be noted that special treatment is required for evaluating elasticities and marginal effects when the explanatory variables include quadratic terms or interaction variables (see the discussion in Wooldridge (2000, p. 533)). A common application is to work with log-transformed variables. The LOG option on the LOGIT command assumes observations are in the form logXkt. 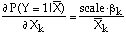Marginal effects at the sample means are then derived from:               Marginal Effects for Dummy Variables Suppose the kth explanatory variable is a 0-1 dummy variable. The change in the probability of a success (Y=1) that results from changing Xk from zero to one, holding all other variables at some fixed values, denoted by X*, is given by the difference:       P(Y=1 | Xk=1 , X*) - P(Y=1 | Xk=0 , X*) Values must be set for X*. An approach is to set values to represent a "typical case". A "typical case" can be defined by setting all dummy variables to their modal values and all other variables to their mean values. The SHAZAM output reports marginal effects for all dummy explanatory variables in the section labelled PROBABILITIES FOR A TYPICAL CASE. For a dummy explanatory variable Xk, the column labelled X=0 reports the probability:       P(Y=1 | Xk=0 , X*) and the column labelled X=1 gives the probability:       P(Y=1 | Xk=1 , X*) The final column labelled MARGINAL EFFECT reports the difference between the two probabilities. The values used for X* are reported in the column labelled CASE VALUES. These are set as the modal values for dummy variables and sample averages for other variables. For the school budget voting study, the variable SCHOOL is a dummy variable equal to one if the individual is employed as a school teacher and zero otherwise. A question to consider is: Are school teachers more likely to vote yes in the school budget referendum, holding all other variables fixed (that is, relative to individuals that are not school teachers but otherwise have similar characteristics) ? The positive estimated coefficient on the school dummy variable indicates a higher probability of a yes vote for a school teacher. To get an estimate of the magnitude of the effect, set the explanatory variables to values that represent a "typical voter" in the sample. The definitions of the variables in the data set can be reviewed. The dummy variables PUB12, PUB34, PUB5 and PRIV all have a mode of zero. This describes a voter with no children in public or private school. This "typical voter" has an income of $23,094 (1973 US$), pays $1,080 in property taxes and 8.5 years residency. An individual that is not a school teacher, with "typical" characteristics on all variables in the model, has a probability of a yes vote of 0.439. If the individual is a school teacher the probability increases to 0.836. The marginal effect is the difference 0.397. Note that the marginal effect obtained using the less precise method of taking the partial derivative with respect to the school dummy variable was calculated to be 0.426.     Overall Significance and Goodness of Fit Measures For the first model in the school budget voting study the SHAZAM output reports the statistics below: LOG-LIKELIHOOD FUNCTION = -55.548 LOG-LIKELIHOOD(0) = -63.037 LIKELIHOOD RATIO TEST = 14.9788 WITH 8 D.F. P-VALUE= 0.05956 Denote the value of the LOG-LIKELIHOOD FUNCTION by logLMAX. Let logL0 denote the value of the restricted log-likelihood when all slope coefficients are zero (LOG-LIKELIHOOD(0)). For a test of the null hypothesis that all slope coefficients are zero, the likelihood ratio test statistic is calculated as:       2 (logLMAX - logL0) Approximate critical values are obtained from the chi-square distribution with degrees of freedom equal to the number of slope coefficients. The SHAZAM output reports a p-value for the test statistic. Inspection of the above output shows that, at a 10% significance level, the null hypothesis is rejected. The final part of the SHAZAM logit estimation output reports a variety of goodness-of-fit measures that have been proposed by various researchers. Formula and references are given in the SHAZAM User's Reference Manual. A useful comment from Wooldridge (2000, p. 536) is: "goodness-of-fit is not usually as important as statistical and economical significance of the explanatory variables." [SHAZAM Guide home]