Ordinary Least Squares Regression
The OLS command will estimate the parameters of a
linear regression equation by the method of ordinary least squares.
The general command format is:
OLS depvar indeps / options
|
where depvar is the dependent variable, indeps is a list of the
explanatory variables and options is a list of desired options.
There are many useful options on the
OLS command and some of these will be illustrated
in this guide.
Examples
- 2-variable Regression Analysis
- Interpreting t-ratios
- Interpreting p-values
- Interpreting elasticities
- The General Linear Statistical Model - Multiple Regression Analysis
Appendixes
- Computing p-values for test statistics
- A Monte Carlo experiment to demonstrate the properties of the OLS estimator
 [SHAZAM Guide home]
[SHAZAM Guide home]
2-variable Regression Analysis
This example uses the Griffiths, Hill and Judge
data set on household expenditure for food.
Consider a simple linear regression with FOOD as the dependent
variable and INCOME as the explanatory variable. The following
SHAZAM program reads the data from the file GHJ.txt,
assigns variable names and runs the regression.
Note that the READ command assumes that the data file
is in the current directory (or folder).
SAMPLE 1 40 READ (GHJ.txt) FOOD INCOME OLS FOOD INCOME STOP |
The output file of results follows.
|
SHAZAM automatically includes an intercept coefficient in the regression
and this is given the name CONSTANT.
On the SHAZAM output, the intercept estimate is listed as the
final coefficient estimate.
The results show that the estimated coefficient on INCOME (the
slope coefficient) is 0.23225 and the intercept estimate
is 7.3832. The estimated equation can be written as:
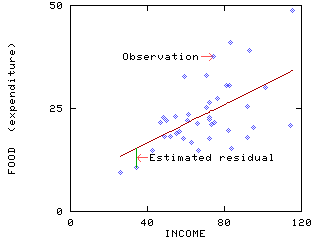
FOOD = 7.38 + 0.232 INCOME + ê
where ê is the estimated residual. The figure below shows a scatterplot of the observations and the estimated regression line. (This figure corresponds to Figure 5.9 of Griffiths, Hill and Judge [1993, p. 187]).
The LIST option on the OLS command
will give more extensive output that includes a listing of the
estimated residuals and the predicted values for the dependent variable.
The use of the LIST option is shown with the SHAZAM
command:
OLS FOOD INCOME / LIST |
The interested reader can look at the
SHAZAM output generated with the LIST option.
Interpreting t-ratios
The OLS estimation results report the ESTIMATED COEFFICIENT
and the estimated STANDARD ERROR.
With the assumption that the errors
are normally distributed these estimates can be used for hypothesis
testing purposes. In the above example, a useful question to ask is:
Is the estimated coefficient on INCOME significantly different
from zero ? That is, does household income have an effect on the level of
household expenditure for food ? To help answer this question the SHAZAM
output reports the test statistic:
T-RATIO = ESTIMATED COEFFICIENT / STANDARD ERROR
The estimated coefficient is significantly different from zero
(that is, the null hypothesis of a zero coefficient is rejected) if the
t-ratio is "relatively large". The critical value is obtained
from tables for the t-distribution with N-K degrees of
freedom (N is the number of observations and
K is the number of estimated
coefficients). These tables are usually printed in the appendix to
econometrics textbooks.
For the household food expenditure example the reported t-ratio for the
coefficient on INCOME is 4.20.
The number of observations is 40 and the number of estimated coefficients
is 2 and so the degrees of freedom (DF) is 38. By choosing a
signficance level of 5% and considering a two-sided test
(so that the critical region in each tail is 2.5%) the critical
value obtained from printed tables is 2.024.
(Note that this critical value was approximated using the tabulated values
for 30 and 40 degrees of freedom that are reported in the tables.)
In absolute value, the t-ratio exceeds this critical value.
Therefore, there is strong evidence to conclude that the estimated coefficient
on INCOME is significantly different from zero.
Interpreting p-values
When interpreting t-ratios it can be inconvenient to consult
statistical tables. To assist the user, SHAZAM
reports the P-VALUE on the OLS estimation output.
This value is computed as the tail probability for a two-tail
test of the null hypothesis that the coefficient is 0.
This is the probability of a Type I error - the probability of
rejecting a true hypothesis.
The null hypothesis is rejected if the p-value is "small" (say smaller than 0.10, 0.05 or 0.01). For example, if the p-value is 0.078, this means that the null hypothesis cannot be rejected at a 5% significance level but can be rejected at a 10% significance level.
Note: SHAZAM only reports three decimal places for the
p-value. So a value that is reported as .000 actually means
a value less than .0005.
This can be interpreted as meaning that the null hypothesis of a
zero coefficient is rejected at any reasonable significance level.
It is possible to use SHAZAM commands to compute p-values for test statistics.
Interpreting elasticities
For the household food expenditure relationship the estimated coefficient
on INCOME measures the marginal effect. This gives the amount
by which FOOD changes in response to a one unit
change in INCOME.
Another measure of interest to economists is elasticity. This
gives the percentage change in the dependent variable that results
from a 1% change in the explanatory variable.
The final column on the SHAZAM OLS estimation output reports the
ELASTICITY AT MEANS.
For the example illustrated here,
let B1 be the estimated coefficient on INCOME
and let CM and PM be the sample means of
FOOD and INCOME respectively.
The income elasticity evaluated at the sample means is computed as:
B1 (PM/CM) = 0.6871
When interpreting the meaning of the estimated coefficients and the elasticities users should take careful note of the units of measurement of the variables in the regression equation.
 [Back to Top]
[Back to Top] |
 [SHAZAM Guide home]
[SHAZAM Guide home] |
The LIST option
The SHAZAM output that follows shows the use of the
LIST option on the OLS command.
|
The LIST option displays a table of results that
contains the following:
OBSERVED VALUE |
The observed value of the dependent variable. |
PREDICTED VALUE |
The predicted value (also called estimated value or fitted value) of the dependent variable. |
CALCULATED RESIDUAL |
The difference between the observed and predicted values. |
The right hand side of the output displays a rough plot of the residuals.
A property of ordinary least squares regression (when an intercept is included) is that the sum of the estimated residuals (and hence the mean of the estimated residuals) is 0. Note that the final part of the SHAZAM output reports:
RESIDUAL SUM = -.36060E-12
That is, SHAZAM computes the sum of residuals as
.00000000000036060. This shows that computer calculations
can have some imprecision. Different computers may have numerical differences
in the reporting of this result.
 [Back to Top]
[Back to Top] |
 [SHAZAM Guide home]
[SHAZAM Guide home] |