Testing for Heteroskedasticity Heteroskedasticity refers to unequal variance in the regression errors. Heteroskedasticity can arise in a variety of ways and a number of tests have been proposed. Typically a test is designed to test the null hypothesis of homoskedasticity (equal error variance) against some specific alternative heteroskedasticity specification. Examples Heteroskedasticity as a function of the explanatory variables Heteroskedasticity as a sample partition More tests for heteroskedasticity A Note on the Spelling of Heteroskedasticity A 'c' is often used instead of a 'k' in the spelling of heteroskedasticity. The research by McCulloch [1985] concludes that the word is derived from Greek roots and the proper English spelling is with a 'k'. Reference: J. Huston McCulloch, "On Heteros*edasticity", Econometrica, Vol. 53, 1985, p. 483. [SHAZAM Guide home] Heteroskedasticity as a function of the explanatory variables Test statistics are reported with the SHAZAM commands: OLS . . . DIAGNOS / HET The DIAGNOS command uses the results from the immediately preceding OLS command to generate diagnostic tests. The HET option computes and reports tests for heteroskedasticity. These tests are obtained by using a function of the OLS residuals et as a dependent variable in an auxiliary regression. A number of alternative auxiliary regressions have been proposed as follows. 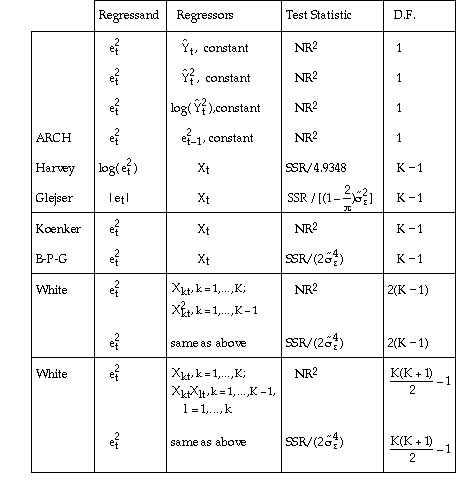where Xt is a (K x 1) vector of observations on the explanatory variables (including the constant) for t=1,...,N. SSE is the sum of squared errors from the initial OLS regression. R2 and SSR are the R-square and the regression sum of squares respectively from the auxiliary regression. Note that the final two auxiliary regressions include cross-products of the explanatory variables as regressors. Therefore, the application requires at least 2 explanatory variables. The final two test statistics are not reported for regressions that specify one explanatory variable. In "large samples" the test statistics have a chi-square distribution with degrees of freedom as given in the D.F. column. This means that critical values can be obtained from tables for the chi-square distribution, but the comparison is approximate only. References for the various test statistics are given in the SHAZAM User's Reference Manual. The ARCH (AutoRegressive Conditional Heteroskedasticity) test is in a different category from the others. This test has specific application to time series data and detects successive periods of volatility followed by successive periods of stability. This type of behaviour has been found in financial time series data. Example Heteroskedasticity has been found to be a feature of cross-section studies on household expenditure. This example, from Griffiths, Hill and Judge, uses a data set on household expenditure. The SHAZAM commands are: SAMPLE 1 40 READ (GHJ.txt) FOOD INCOME OLS FOOD INCOME DIAGNOS / HET STOP The SHAZAM output can be inspected. The results from the DIAGNOS / HET command are: HETEROSKEDASTICITY TESTS CHI-SQUARE D.F. P-VALUE TEST STATISTIC E**2 ON YHAT: 12.042 1 0.00052 E**2 ON YHAT**2: 13.309 1 0.00026 E**2 ON LOG(YHAT**2): 10.381 1 0.00127 E**2 ON LAG(E**2) ARCH TEST: 2.565 1 0.10926 LOG(E**2) ON X (HARVEY) TEST: 4.358 1 0.03683 ABS(E) ON X (GLEJSER) TEST: 11.611 1 0.00066 E**2 ON X TEST: KOENKER(R2): 12.042 1 0.00052 B-P-G (SSR) : 11.283 1 0.00078 E**2 ON X X**2 (WHITE) TEST: KOENKER(R2): 14.582 2 0.00068 B-P-G (SSR) : 13.662 2 0.00108 The 5% critical value from a chi-square distribution with 1 degree of freedom is 3.84. With the exception of the ARCH test, all test statistics exceed this value and so there is evidence for heteroskedasticity in the estimated residuals. Of course, the ARCH test is of no relevance to this example since the data is cross-section data and the ARCH test has application to time series data. Note that the first test statistic and the seventh test statistic are identical. As an exercise the user should verify that these tests are always identical when the regression contains one explanatory variable. [SHAZAM Guide home] SHAZAM output with tests for heteroskedasticity The OLS estimation results are described in further detail in Griffiths, Hill and Judge [1993, Section 5.3.2]. |_SAMPLE 1 40 |_READ (GHJ.txt) FOOD INCOME UNIT 88 IS NOW ASSIGNED TO: GHJ.txt 2 VARIABLES AND 40 OBSERVATIONS STARTING AT OBS 1 |_OLS FOOD INCOME OLS ESTIMATION 40 OBSERVATIONS DEPENDENT VARIABLE = FOOD ...NOTE..SAMPLE RANGE SET TO: 1, 40 R-SQUARE = .3171 R-SQUARE ADJUSTED = .2991 VARIANCE OF THE ESTIMATE-SIGMA**2 = 46.853 STANDARD ERROR OF THE ESTIMATE-SIGMA = 6.8449 SUM OF SQUARED ERRORS-SSE= 1780.4 MEAN OF DEPENDENT VARIABLE = 23.595 LOG OF THE LIKELIHOOD FUNCTION = -132.672 VARIABLE ESTIMATED STANDARD T-RATIO PARTIAL STANDARDIZED ELASTICITY NAME COEFFICIENT ERROR 38 DF P-VALUE CORR. COEFFICIENT AT MEANS INCOME .23225 .5529E-01 4.200 .000 .563 .5631 .6871 CONSTANT 7.3832 4.008 1.842 .073 .286 .0000 .3129 |_DIAGNOS / HET DEPENDENT VARIABLE = FOOD 40 OBSERVATIONS REGRESSION COEFFICIENTS 0.232253330328 7.38321754308 HETEROSKEDASTICITY TESTS CHI-SQUARE D.F. P-VALUE TEST STATISTIC E**2 ON YHAT: 12.042 1 0.00052 E**2 ON YHAT**2: 13.309 1 0.00026 E**2 ON LOG(YHAT**2): 10.381 1 0.00127 E**2 ON LAG(E**2) ARCH TEST: 2.565 1 0.10926 LOG(E**2) ON X (HARVEY) TEST: 4.358 1 0.03683 ABS(E) ON X (GLEJSER) TEST: 11.611 1 0.00066 E**2 ON X TEST: KOENKER(R2): 12.042 1 0.00052 B-P-G (SSR) : 11.283 1 0.00078 E**2 ON X X**2 (WHITE) TEST: KOENKER(R2): 14.582 2 0.00068 B-P-G (SSR) : 13.662 2 0.00108 |_STOP [SHAZAM Guide home]