SHAZAM Pooling by OLS

Pooling by OLS with Panel-Corrected Standard Errors and Dummy Variables

The time series observations for all the cross-section units can be pooled and the regression coefficients can be estimated by OLS.
Cross-section differences can be recognized by allowing different intercepts. Cross-section dummy variables are included as regressors and the equation is estimated by OLS. This is known as a fixed effects model.
On the POOL command, the following options are available for pooled OLS estimation:

OLS Estimation by pooled OLS.

HETCOV Estimation by pooled OLS with computation of a panel-corrected covariance matrix of the coefficient estimates.

Panel Corrected Standard Errors

It may be realistic to expect different error variances for the different cross-sections. For example, Greene [2000, p. 594] notes that for a cross-country comparison there may be variation in the scales of the variables in the model. It may also be realistic to expect cross-section contemporaneous error correlation. For the investment demand data set Greene [2000, p. 599] observes:
. . . we have two automobile producers, two major suppliers to the electric utility industry, and one major supplier to all four of the others, U.S. Steel. It is very likely that the macroeconomic factors that affect these firms affect all of them to varying degrees. For the auto industry, the fates of GM and Chrysler are obviously tied both to the economy as a whole and to factors that are specific to the two firms. As such, it would seem reasonable to allow correlation of the disturbances across firms.

With cross-section heteroskedasticity the OLS standard errors will be inconsistent. A method for computing a heteroskedastic-consistent covariance matrix for pooled regression models is discussed in Beck and Katz [1995], Beck et al. [1993] and Greene [2000, p. 594].
The Beck and Katz covariance matrix estimate gives "Panel Corrected Standard Errors" (PCSE). Note that the HETCOV option on the OLS command will compute heteroskedasticity consistent standard errors -- but this computation will not take into account the panel structure of the errors. The PCSE formula is specifically designed for panel data.
The panel corrected standard errors are obtained as the square roots of the diagonal elements of the matrix:
cov(b) = (X'X)^-1 (X'( 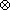Phi I_T)X) (X'X)^-1

where Phi is an N x N matrix with the (i,j)th element estimated by:

( sum _t^{^T}₌₁ ê_i,tê_j,t ) / T

Lagrange Multiplier Tests
The SHAZAM output reports a Lagrange multiplier statistic for testing for cross-section heteroskedasticity as suggested by Greene [2000, p. 596]. The output also reports the Breusch-Pagan Lagrange multiplier statistic for a test for a diagonal covariance matrix (that is, no cross-secion correlation). See Greene [2000, Equation 15-14, p. 601]
Example

The SHAZAM commands (filename: FIRM.SHA) below first estimate an investment demand equation by pooled OLS. The estimation is repeated with the HETCOV option to obtain the standard errors that are corrected for cross-section heteroskedasticity and contemporaneous correlation. The analysis is then extended by incorporating cross-section dummy variables to allow for different firm intercepts.

SAMPLE 1 20 READ(FIRM1.txt) YEAR IGM FGM CGM ICHR FCHR CCHR / SKIPLINES=1 READ(FIRM2.txt) YEAR IGE FGE CGE IWH FWH CWH / SKIPLINES=1 READ(FIRM3.txt) YEAR IUS FUS CUS / SKIPLINES=1 * Stack the data MATRIX I=(IGM'|ICHR'|IGE'|IWH'|IUS')' MATRIX F=(FGM'|FCHR'|FGE'|FWH'|FUS')' MATRIX C=(CGM'|CCHR'|CGE'|CWH'|CUS')' SAMPLE 1 100 * Pooling by OLS POOL I F C / NCROSS=5 OLS DN * Pooling by OLS with Panel-Corrected Covariance Matrix POOL I F C / NCROSS=5 OLS HETCOV * Generate a cross-section index * Set the number of time periods GEN1 NT=20 GENR CSINDEX=SUM(SEAS(NT)) * Get standard errors with correction for heteroskedasiticity but * assume the restriction of no cross-section correlation. POOL I F C / NCROSS=5 OLS HETCOV CSINDEX=CSINDEX * Now get the White standard errors OLS I F C / HETCOV * Create cross-section dummy variables. * Set the number of cross-sections GEN1 NC=5 MATRIX CSDUM=SEAS(100,-NC) DO #=1,NC GENR D#=CSDUM:# ENDO * OLS estimation with dummy variables POOL I F C D1-D5 / NOCONSTANT NCROSS=5 OLS HETCOV RSTAT * Test for equality of firm intercepts TEST TEST D1=D2 TEST D1=D3 TEST D1=D4 TEST D1=D5 END STOP

On the first POOL command the DN option ensures that no degrees of freedom adjustment is used in the computation of the variance-covariance matrix of the parameter estimates.
The above SHAZAM program shows a general method for generating cross-section dummy variables. The SHAZAM output can be viewed.
Test statistics calculated from the pooled OLS residuals are:

Test statistic 5% critical value
from the chi-square
distribution
Test for cross-section
heteroskedasticity 46.63 9.49

Test for cross-section
correlation 50.68 18.31

The first test statistic exceeds the critical value. Therefore, the null hypothesis of homoskedasticity is rejected (see Greene [2000, p. 598]). The second test statistic is computed from the OLS residuals. Greene [2000, p. 601] suggests that there may be some limitations to the interpretation of this test statistic.
The table below shows the pooled OLS estimates with a comparison of alternative standard errors. These results can be compared with Greene [2000, Example 15.2, p. 594 and Table 15.1, p. 598].

Variable
name Coefficient
Estimate Standard Errors

OLS PCSE HET White

F 0.105 0.0112 0.0083 0.0091 0.0091

C 0.305 0.0429 0.0330 0.0409 0.0591

intercept -48.030 21.1555 10.8144 14.2037 15.0167

The standard errors in the PCSE column are the Beck-Katz standard errors (reported in Greene [2000, Example 15.2, p. 594]). The standard errors in the HET column are the standard errors that assume no cross-section correlation (reported in the "Correct" column of Greene [2000, Table 15.1, p. 598]).
Now consider the estimation results for the fixed effects model. A separate dummy variable is included for each firm and the NOCONSTANT option is specified on the POOL command. This is required to avoid the "dummy variable trap". Based on the OLS estimated residuals, the test statistic for cross-section heteroskedasticity is 33.5. This is significant. The estimation results report the panel-corrected standard errors.
Following model estimation the TEST command is used to test the null hypothesis of equality of the firm intercepts against the alternative hypothesis of some differences. The F-test statistic is 63.5 to give strong evidence to reject the null hypothesis. Note that since the HETCOV option was specified on the POOL command that precedes the TEST command the panel-corrected covariance matrix is used in the computation of the F-test statistic.
Testing for autocorrelation

It is also of interest to test for autocorrelation within cross-section units. The RSTAT option on the POOL command reports a Durbin-Watson statistic for pooled data. Suppose ê are the OLS residuals. The Durbin-Watson test statistic is calculated as:
sum _i^{^N}₌₁ sum _t^{^T}₌₂ (ê_it - ê_i,t-1)² / sum _i^{^N}₌₁ sum _t^{^T}₌₁ ê_it²
The value for RHO that is printed on the same output line as the Durbin-Watson statistic is calculated as:
sum _i^{^N}₌₁ sum _t^{^T}₌₂ ê_itê_i,t-1 / sum _i^{^N}₌₁ sum _t^{^T}₌₂ (ê_i,t-1)²

The estimation results for OLS with dummy variables report the Durbin-Watson statistic 0.7745. For the fixed effects model, a p-value for the Durbin-Watson test can be computed. For this example, the low value of the Durbin-Watson statistic gives evidence for model misspecification.

[SHAZAM Guide home]

SHAZAM output

|_SAMPLE 1 20 |_READ(FIRM1.txt) YEAR IGM FGM CGM ICHR FCHR CCHR / SKIPLINES=1 UNIT 88 IS NOW ASSIGNED TO: FIRM1.txt 7 VARIABLES AND 20 OBSERVATIONS STARTING AT OBS 1 |_READ(FIRM2.txt) YEAR IGE FGE CGE IWH FWH CWH / SKIPLINES=1 UNIT 88 IS NOW ASSIGNED TO: FIRM2.txt 7 VARIABLES AND 20 OBSERVATIONS STARTING AT OBS 1 |_READ(FIRM3.txt) YEAR IUS FUS CUS / SKIPLINES=1 UNIT 88 IS NOW ASSIGNED TO: FIRM3.txt 4 VARIABLES AND 20 OBSERVATIONS STARTING AT OBS 1 |_* Stack the data |_MATRIX I=(IGM'|ICHR'|IGE'|IWH'|IUS')' |_MATRIX F=(FGM'|FCHR'|FGE'|FWH'|FUS')' |_MATRIX C=(CGM'|CCHR'|CGE'|CWH'|CUS')' |_SAMPLE 1 100 |_* Pooling by OLS |_POOL I F C / NCROSS=5 OLS DN POOLED CROSS-SECTION TIME-SERIES ESTIMATION 100 TOTAL OBSERVATIONS 5 CROSS-SECTIONS 20 TIME-PERIODS DEPENDENT VARIABLE = I THE DN OPTION IS IN EFFECT POOLING BY OLS LM TEST FOR CROSS-SECTION HETEROSKEDASTICITY 46.630 CHI-SQUARE WITH 4 D.F. P-VALUE= 0.00000 BREUSCH-PAGAN LM TEST FOR DIAGONAL COVARIANCE MATRIX 50.682 CHI-SQUARE WITH 10 D.F. P-VALUE= 0.00000 R-SQUARE = 0.7789 VARIANCE OF THE ESTIMATE-SIGMA**2 = 15709. STANDARD ERROR OF THE ESTIMATE-SIGMA = 125.33 SUM OF SQUARED ERRORS-SSE= 0.15709E+07 MEAN OF DEPENDENT VARIABLE = 248.96 LOG OF THE LIKELIHOOD FUNCTION = -624.993 ASYMPTOTIC VARIABLE ESTIMATED STANDARD T-RATIO PARTIAL STANDARDIZED ELASTICITY NAME COEFFICIENT ERROR -------- P-VALUE CORR. COEFFICIENT AT MEANS F 0.10509 0.1121E-01 9.378 0.000 0.690 0.5574 0.8114 C 0.30537 0.4285E-01 7.126 0.000 0.586 0.4236 0.3815 CONSTANT -48.030 21.16 -2.270 0.023-0.225 0.0000 -0.1929 |_* Pooling by OLS with Panel-Corrected Covariance Matrix |_POOL I F C / NCROSS=5 OLS HETCOV POOLED CROSS-SECTION TIME-SERIES ESTIMATION 100 TOTAL OBSERVATIONS 5 CROSS-SECTIONS 20 TIME-PERIODS DEPENDENT VARIABLE = I POOLING BY OLS USING PANEL-CORRECTED COVARIANCE MATRIX LM TEST FOR CROSS-SECTION HETEROSKEDASTICITY 46.630 CHI-SQUARE WITH 4 D.F. P-VALUE= 0.00000 BREUSCH-PAGAN LM TEST FOR DIAGONAL COVARIANCE MATRIX 50.682 CHI-SQUARE WITH 10 D.F. P-VALUE= 0.00000 R-SQUARE = 0.7789 VARIANCE OF THE ESTIMATE-SIGMA**2 = 16195. STANDARD ERROR OF THE ESTIMATE-SIGMA = 127.26 SUM OF SQUARED ERRORS-SSE= 0.15709E+07 MEAN OF DEPENDENT VARIABLE = 248.96 LOG OF THE LIKELIHOOD FUNCTION = -624.993 VARIABLE ESTIMATED STANDARD T-RATIO PARTIAL STANDARDIZED ELASTICITY NAME COEFFICIENT ERROR 97 DF P-VALUE CORR. COEFFICIENT AT MEANS F 0.10509 0.8318E-02 12.63 0.000 0.789 0.5574 0.8114 C 0.30537 0.3304E-01 9.242 0.000 0.684 0.4236 0.3815 CONSTANT -48.030 10.81 -4.441 0.000-0.411 0.0000 -0.1929 |_* Generate a cross-section index |_* Set the number of time periods |_GEN1 NT=20 |_GENR CSINDEX=SUM(SEAS(NT)) |_* Get standard errors with correction for heteroskedasiticity but |_* assume the restriction of no cross-section correlation. |_POOL I F C / NCROSS=5 OLS HETCOV CSINDEX=CSINDEX POOLED CROSS-SECTION TIME-SERIES ESTIMATION 100 TOTAL OBSERVATIONS 5 CROSS-SECTIONS UNBALANCED PANELS TIME-PERIODS 1 20 2 20 3 20 4 20 5 20 DEPENDENT VARIABLE = I POOLING BY OLS USING PANEL-CORRECTED COVARIANCE MATRIX R-SQUARE = 0.7789 VARIANCE OF THE ESTIMATE-SIGMA**2 = 16195. STANDARD ERROR OF THE ESTIMATE-SIGMA = 127.26 SUM OF SQUARED ERRORS-SSE= 0.15709E+07 MEAN OF DEPENDENT VARIABLE = 248.96 LOG OF THE LIKELIHOOD FUNCTION = -624.993 VARIABLE ESTIMATED STANDARD T-RATIO PARTIAL STANDARDIZED ELASTICITY NAME COEFFICIENT ERROR 97 DF P-VALUE CORR. COEFFICIENT AT MEANS F 0.10509 0.9063E-02 11.60 0.000 0.762 0.5574 0.8114 C 0.30537 0.4095E-01 7.458 0.000 0.604 0.4236 0.3815 CONSTANT -48.030 14.20 -3.382 0.001-0.325 0.0000 -0.1929 |_* Now get the White standard errors |_OLS I F C / HETCOV OLS ESTIMATION 100 OBSERVATIONS DEPENDENT VARIABLE= I ...NOTE..SAMPLE RANGE SET TO: 1, 100 USING HETEROSKEDASTICITY-CONSISTENT COVARIANCE MATRIX R-SQUARE = 0.7789 R-SQUARE ADJUSTED = 0.7743 VARIANCE OF THE ESTIMATE-SIGMA**2 = 16195. STANDARD ERROR OF THE ESTIMATE-SIGMA = 127.26 SUM OF SQUARED ERRORS-SSE= 0.15709E+07 MEAN OF DEPENDENT VARIABLE = 248.96 LOG OF THE LIKELIHOOD FUNCTION = -624.993 VARIABLE ESTIMATED STANDARD T-RATIO PARTIAL STANDARDIZED ELASTICITY NAME COEFFICIENT ERROR 97 DF P-VALUE CORR. COEFFICIENT AT MEANS F 0.10509 0.9146E-02 11.49 0.000 0.759 0.5574 0.8114 C 0.30537 0.5911E-01 5.166 0.000 0.465 0.4236 0.3815 CONSTANT -48.030 15.02 -3.198 0.002-0.309 0.0000 -0.1929 |_* Create cross-section dummy variables. |_* Set the number of cross-sections |_GEN1 NC=5 |_MATRIX CSDUM=SEAS(100,-NC) |_DO #=1,NC |_ GENR D#=CSDUM:# |_ENDO _DO #=1,NC ****** EXECUTION BEGINNING FOR DO LOOP # = 1 #_ GENR D1=CSDUM:1 #_ ENDO #_ GENR D2=CSDUM:2 #_ ENDO #_ GENR D3=CSDUM:3 #_ ENDO #_ GENR D4=CSDUM:4 #_ ENDO #_ GENR D5=CSDUM:5 #_ ENDO ****** EXECUTION FINISHED FOR DO LOOP #= 5 |_* OLS estimation with dummy variables |_POOL I F C D1-D5 / NOCONSTANT NCROSS=5 OLS HETCOV RSTAT POOLED CROSS-SECTION TIME-SERIES ESTIMATION 100 TOTAL OBSERVATIONS 5 CROSS-SECTIONS 20 TIME-PERIODS DEPENDENT VARIABLE = I POOLING BY OLS USING PANEL-CORRECTED COVARIANCE MATRIX LM TEST FOR CROSS-SECTION HETEROSKEDASTICITY 33.468 CHI-SQUARE WITH 4 D.F. P-VALUE= 0.00000 BREUSCH-PAGAN LM TEST FOR DIAGONAL COVARIANCE MATRIX 28.322 CHI-SQUARE WITH 10 D.F. P-VALUE= 0.00160 R-SQUARE = 0.9375 VARIANCE OF THE ESTIMATE-SIGMA**2 = 4777.3 STANDARD ERROR OF THE ESTIMATE-SIGMA = 69.118 SUM OF SQUARED ERRORS-SSE= 0.44429E+06 MEAN OF DEPENDENT VARIABLE = 248.96 LOG OF THE LIKELIHOOD FUNCTION = -561.847 VARIABLE ESTIMATED STANDARD T-RATIO PARTIAL STANDARDIZED ELASTICITY NAME COEFFICIENT ERROR 93 DF P-VALUE CORR. COEFFICIENT AT MEANS F 0.10598 0.1771E-01 5.985 0.000 0.527 0.5621 0.8183 C 0.34666 0.2716E-01 12.76 0.000 0.798 0.4808 0.4331 D1 -76.067 74.99 -1.014 0.313-0.105 -0.1142 -0.0611 D2 -29.374 11.93 -2.462 0.016-0.247 -0.0441 -0.0236 D3 -242.17 35.36 -6.849 0.000-0.579 -0.3635 -0.1945 D4 -57.899 12.77 -4.534 0.000-0.425 -0.0869 -0.0465 D5 92.539 39.35 2.352 0.021 0.237 0.1389 0.0743 DURBIN-WATSON = 0.7745 VON NEUMANN RATIO = 0.7823 RHO = 0.60606 RESIDUAL SUM = 0.41922E-11 RESIDUAL VARIANCE = 4777.3 SUM OF ABSOLUTE ERRORS= 4782.7 R-SQUARE BETWEEN OBSERVED AND PREDICTED = 0.9375 |_* Test for equality of firm intercepts |_TEST |_ TEST D1=D2 |_ TEST D1=D3 |_ TEST D1=D4 |_ TEST D1=D5 |_END F STATISTIC = 63.486725 WITH 4 AND 93 D.F. P-VALUE= 0.00000 WALD CHI-SQUARE STATISTIC = 253.94690 WITH 4 D.F. P-VALUE= 0.00000 UPPER BOUND ON P-VALUE BY CHEBYCHEV INEQUALITY = 0.01575 |_STOP

[SHAZAM Guide home]